算法思想

口诀 # 

难题首选动归
受阻贪心暴力
考虑分治思想
配合排序哈希

递归(recursion) # 

介绍
    利用递归，把状态的管理责任推给运行时
递归转迭代
    可加上memory做优化

分治(divide and conquer) # 

介绍
    广义分治法
例子
    二分检索
    找最大/最小元素
    归并分类
    快速分类
    选择问题
    斯特拉森矩阵乘法

贪心(greedy) # 

案例
    Dijkstra最短路径
    最小生成树Prim, Kruskal

    背包问题
    作业排序
    最优归并模式

动态规划(dynamic planning) # 

方法
    常用滚动数组降低空间复杂度
案例
    多段图
    结点间最短路径
    最优二叉检索树
    0/1背包问题
    可靠性设计
    货郎担问题(旅行商问题)
    流水线调度问题

检索与周游(retrieval/travel) # 

案例
    深度优先检索
    广度优先检索
    与/或图
    对策树

回溯(backtracking) # 

案例
    8皇后问题
    图的着色
    哈密顿环
    背包问题

暴力(brute force) # 

介绍
    分支限界条件加快效率
例子
    DFS, BFS
  • 分支-限界(branch and bound) 案例 LC检索 0/1背包问题 货郎担问题

并行(parallel) #

时间复杂度(time complexity) # 

O()表示上界(<=), Ω() [omega]表示下界(>=), Θ() [Theta] 表示上下界相同, o()表示非Θ()的O()
    N >= n0时, T(N) <= cf(N), 记为T(N) = O(f(N))
    N >= n0时, T(N) >= cg(N), 记为T(N) = Ω(g(N))
    T(N) = Θ(h(N)) 当且仅当T(N) = O(h(N)) 和 T(N) = Ω(h(N))
上界(upper bound)
下界(lower bound)
法则
    # 约定, 不存在特定的时间单位
    # 约定, 机器模型中, 1. 所有指令顺序执行。2. 任一简单的工作都恰好花费一个时间单位
    ## 假设不存在如矩阵求逆或排序这样的单位操作
    1. 如果T1(N) = O(f(N)), T2(N) = O(g(N)), 那么
        T1(N) + T2(N) = O(f(N) + g(N)), 或写成 max(O(f(N)), O(g(N)))
        T1(N) * T2(N) = O(f(N) * g(N))
    2. 如果T(N)是一个k次多项式, 则T(N) = Θ(N^k)
    3. 对任意常数k, (logk) * N = O(N)
        # 对数增长得非常缓慢
一般法则
    1. for 循环时间, 为内部语句的运行时间 * 迭代次数
    2. 嵌套for 循环, 内部语句时间 * 迭代次数n次方
    3. 顺序语句, 各语句时间求和
    4. if(S1)/else(S2), 判断的运行时间加 S1和S2中时间长者
相对增长率(relative rate of growth)
    lim(N->∞)f(N)/g(N)来确定两个函数的相对增长率
        1. 极限是0, 则f(N) = o(g(N))
        2. 极限是c<>0, 则f(N) = Θ(g(N))
        3. 极限是∞, 则g(N) = o(f(N))
        4. 极限摆动，则f(N)与g(N)无关
    洛必达法则
        lim(N->∞)f(N) = ∞, 且lim(N->∞)g(N) = ∞ 时, lim(N->∞)f(N)/g(N) = lim(N->∞)f'(N)/g'(N)
多项式时间算法
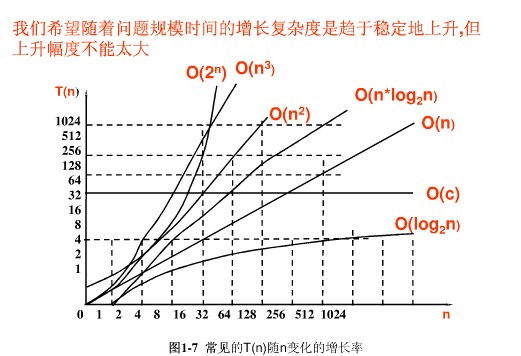
    O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3)
指数时间算法
    O(2^n) < O(n!) < O(n^n)

时间复杂度

递归分析
    1. 如求factorial(阶乘)的简单for循环, 则为O(N)
    2. 求解一个递推关系, 如fabonacii, return fib(n - 1) + fib(n - 2)
        T(N) = T(N - 1) + T(N - 2) + 2, 又fib(N) = fib(N - 1) + fib(N - 2), 由归纳法得T(N) >= fib(N)
        又fib(N) < (5/3)^N, 可知时间指数增长
            # 该算法大量重复计算, 违反递归的合成效益法则
    3. 对于T(N) = aT(N / b) + Θ(N^k), 解为
        O(N^(log(b)(a))), 若 a > b^k
        O(N^k * logN), 若 a = b^k
        O(N^k), 若 a < b^k
影响性能的其它因素
    程序实现方法和语言
    数据读入

空间复杂度(space complexity) # 

Space(N) = Heap(N) + Stack(N), 忽略低次项、系数
    # Heap表示额外申请堆内存空间大小, Stack表示函数栈的最大深度
Jul 31, 2022
Edit this page