 Oct 8, 2018
Oct 8, 2018
口诀
#
难题首选动归
受阻贪心暴力
考虑分治思想
配合排序哈希
递归(recursion)
#
介绍
利用递归,把状态的管理责任推给运行时
递归转迭代
可加上memory做优化
分治(divide and conquer)
#
介绍
广义分治法
例子
二分检索
找最大/最小元素
归并分类
快速分类
选择问题
斯特拉森矩阵乘法
贪心(greedy)
#
案例
Dijkstra最短路径
最小生成树Prim, Kruskal
背包问题
作业排序
最优归并模式
动态规划(dynamic planning)
#
方法
常用滚动数组降低空间复杂度
案例
多段图
结点间最短路径
最优二叉检索树
0/1背包问题
可靠性设计
货郎担问题(旅行商问题)
流水线调度问题
检索与周游(retrieval/travel)
#
案例
深度优先检索
广度优先检索
与/或图
对策树
回溯(backtracking)
#
案例
8皇后问题
图的着色
哈密顿环
背包问题
暴力(brute force)
#
介绍
分支限界条件加快效率
例子
DFS, BFS
- 分支-限界(branch and bound)
案例
LC检索
0/1背包问题
货郎担问题
并行(parallel)
#
时间复杂度(time complexity)
#
O()表示上界(<=), Ω() [omega]表示下界(>=), Θ() [Theta] 表示上下界相同, o()表示非Θ()的O()
N >= n0时, T(N) <= cf(N), 记为T(N) = O(f(N))
N >= n0时, T(N) >= cg(N), 记为T(N) = Ω(g(N))
T(N) = Θ(h(N)) 当且仅当T(N) = O(h(N)) 和 T(N) = Ω(h(N))
上界(upper bound)
下界(lower bound)
法则
# 约定, 不存在特定的时间单位
# 约定, 机器模型中, 1. 所有指令顺序执行。2. 任一简单的工作都恰好花费一个时间单位
## 假设不存在如矩阵求逆或排序这样的单位操作
1. 如果T1(N) = O(f(N)), T2(N) = O(g(N)), 那么
T1(N) + T2(N) = O(f(N) + g(N)), 或写成 max(O(f(N)), O(g(N)))
T1(N) * T2(N) = O(f(N) * g(N))
2. 如果T(N)是一个k次多项式, 则T(N) = Θ(N^k)
3. 对任意常数k, (logk) * N = O(N)
# 对数增长得非常缓慢
一般法则
1. for 循环时间, 为内部语句的运行时间 * 迭代次数
2. 嵌套for 循环, 内部语句时间 * 迭代次数n次方
3. 顺序语句, 各语句时间求和
4. if(S1)/else(S2), 判断的运行时间加 S1和S2中时间长者
相对增长率(relative rate of growth)
lim(N->∞)f(N)/g(N)来确定两个函数的相对增长率
1. 极限是0, 则f(N) = o(g(N))
2. 极限是c<>0, 则f(N) = Θ(g(N))
3. 极限是∞, 则g(N) = o(f(N))
4. 极限摆动,则f(N)与g(N)无关
洛必达法则
lim(N->∞)f(N) = ∞, 且lim(N->∞)g(N) = ∞ 时, lim(N->∞)f(N)/g(N) = lim(N->∞)f'(N)/g'(N)
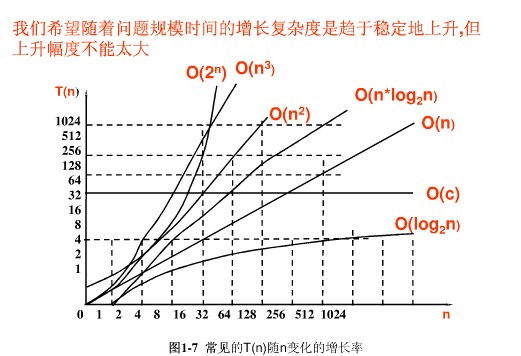
多项式时间算法
O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3)
指数时间算法
O(2^n) < O(n!) < O(n^n)
...
 Oct 7, 2018
Oct 7, 2018
线性
#
列表(list)
数组(array)
# 相同数据类型元素的序列,下标(index)访问
low high
字符串
二进制串(binary string)
# 位串(bit string)
链表(linked list)
节点(node)
指针(pointer)
表头(header)
单链表(singly linked list)
双链表(doubly linked list)
栈(stack)
# 插入和删除只能在端部进行的列表,应用于递归
栈顶(top)
LIFO last-in-first-out
队列(queue)
队头(front)
队尾(rear)
入队(enqueue)
FIFO first-in-first-out
优先队列(priority queue)
# 数据项多来自于全序域(常整数或实数)
查找最大元素,删除最大元素,插入新元素
堆(heap)实现
散列表
#
介绍
有序输入时,树效率低,如果不要求查找有序结果,可以用散列
概念
hash table
hashing(散列)
item(项)
key(关键字)
# 项中某部分
hash function(散列函数)
# 映射函数
collsion(冲突)
# 多个关键字散列到同项的状况
load factor(装填因子)
# λ 元素个数对表长度的比,
# 如果散列是均匀的,表示了一个项中关键字的平均长度
# 一次成功查找要遍历约1 + (λ / 2)个链,1表示被匹配的项
rehashing(再散列)
一半时进行
直到插入失败再进行
middle-of-the-road
# 到达某load factor时进行
caching the hash code(闪存散列代码)
算法
separate chaining(分离链接法)
# 解决冲突
probing hash table(探测散列表)
线性探测法
primary clustering(聚集)
# 线性探测法中形成数据区块
平方探测法
secondary clustering(二次聚集)
# 模拟结果指出,对每次查找,会引起另外的少于一半的探测
double hashing(双散列)
# 模拟表明, 两个散列都mod质数时,探测次数几乎和随机冲突解决方法相同
extendible hashing(可扩散列)
D directory(目录)
# 一个分区中bit的个数,所以M最多2^D
性质
# 基于位模式(bit patterm)是均匀分布的事实, 是"分支系数(branch factor)", N 是记录总数(随时间变化)
树叶期望个数为(N/M)log(2)(e)
所以平均树叶满的程度为ln2 = 0.69, 同B树
目录期望大小为O(N^(1 + 1 / M) / M)
叶子可以指向实际记录的链表(内存装不下太大目录时),这样得到实际数据就需要第二次磁盘访问
队列
#
介绍
queue 先进先出
概念
enqueue(入队)
dequeue(出队)
priority queue(优先队列)
insert
deleteMin
binomial queue(二项队列)
merge, insert, deleteMin 最坏时间为O(logN), 插入花费常数时间
堆序树(二项树)的森林实现
B0 = 2^0, B1 = 2^1, B2 = 2^2 ...
Bn = B0 + B1 + ... B(n-1)
集合
#
概念
set(集合),互不相同项的无序组合(可空)
element(元素)
dictionary(字典),能够查找,增加,删除元素的集合
# 实现时要达到效率的平衡
set union problem(集合合并问题)
# 动态地把n个元素集合划分为一系列不相交的子集
ADT abstract data type(抽象数据类型)
# 由表示数据项的抽象对象集合和一系列对它的操作构成
实现
universal set(通用集合)
通用集合的子集,用长度为n(通用集合的长度)的位向量(bit vector)表示
# 占用大量存储空间
线性列表
# 去除包含的重复元素
# 列表是有序的,但这差别并不重要
多重集(multiset)、包(bag)
# 可重复项的无序组合
表示
S = {2, 3, 5, 7}
S = {n: n 为小于0的质数}
概念
tree
free tree(自由树),连通无回路的图
full tree(满树),所有节点要么是树叶,要么是两个儿子
forest(森林),无回路但不一定连通的图
root
rooted tree(有根树),确定根的树,常简称为树
node
ancestor(祖先),顶点本身也作为自己的祖先
proper ancestor(真祖先),除了自己的祖先
parent(父母)
child(子女)
sibling(兄弟)
leaf(叶节点), 没有子女的顶点
parental(父节点),至少有一个子女的顶点
descendant(子孙),以v为祖先的所有节点,包含v
proper descendant(真子孙),不包含本身
subtree(子树)
depth(深度),从根到v简单路径的长度
height depth 树中结点的最大级数
rank(秩)
# 子女数
height(高度),从根到叶节点最长简单路径的长度
# 按树的层的数量定义时,高度增加1
degree(度,一个节点子树的数目)
level(root为1级, 结点为p级时,儿子在p+1级)
state-space tree(状态空间树),可用于分析回溯和分支界限
ordered tree(有序树),有根树的每个顶点,所有子女有序
first child-next sibling representation(先子女后兄弟表示法)
# 子女数不定,父节点只存第一个子女,该子女存兄弟链表
## 以一种高效方式将有序树改造成关联二叉树
## 关联二叉树中,左指针表示下层,右指针表示兄弟节点
binary tree(二叉树),属于有序树
left child(左子女)
right child(右子女)
左(右)子树
# 二叉树可以递归定义,所有可以用递归算法
binary search tree(二叉查找树),父母顶点比左子树中所有数字大,右子树中小
效率,多取决于高度
logn <= h <= n - 1
# h 为高度, n为顶点数
multiway search tree(多路查找树)
B树, B+树, B-树
边
树向边
回边
前向边
# 顶点到非子孙
交叉边
# 非前三都是交叉边
性质
|E| = |V| - 1
# 树的边数总比顶点数小1
# 图变树的必要不充分条件,连通图变树的必要充分条件
任意两个顶点间总存在简单路径,任选顶点可作根
二叉树
#
介绍
binary tree
常用顺序表或链表存储
概念
full binary tree(满二叉树)
# 满子节点,且子节点在同一层上
heap(堆)
# 根向下从大到小排序
binary search tree(二分检索树)
# 左子节点小于父节点小于右子节点
left child(左子女)
right child(右子女)
左(右)子树
# 二叉树可以递归定义,所有可以用递归算法
complete binary tree(完全二叉树)
# 只有最大层节点不满且连续集中在左边
高是logN
可以用数组实现(从index = 1开始存储)
左儿子在2i, 右儿子在2i + 1, 父亲在i / 2
perfect binary tree(理想二叉树)
# 满节点二叉树
full binary tree(满二叉树)
# 同理想二叉树
skewed tree(斜树)
# 一个节点不断左斜是左斜树,相反为右斜树
binary search tree(二叉查找树)
# 父母顶点比左子树中所有数字大,右子树中小
AVL tree(Adelson-Velskii-Landis tree)
# 带有平衡条件(balance condition)的二叉查找树
平衡条件: 左右子树最多差1
# 节点中存储高度信息
splay tree(伸展树)
# 分析树的一种
效率,多取决于高度
logn <= h <= n - 1
# h 为高度, n为顶点数
树转换二叉树
概念
binary heap(二叉堆、堆)
# 一棵完全二叉树
结构性
heap-order property(堆序性)
heap-order tree(堆序树)
已证明,平均一次插入需要2.607次比较,所以上移1.607层
d-堆
# 二叉堆是2-堆
deleteMin为时间为O(dlog(d)(N))
实践中
插入次数比deleteMin次数多(可加速)
主存不够时如B树使用
4-堆胜过二叉堆
leftist heap(左式堆)
不是理想平衡(perfectly balanced)的,实际趋向于不平衡
具有堆序性
npl(X) null path length 零路径长
# X到一个不具有两个儿子节点的最短路径。到本身npl(X) = 0。npl(null) = -1
o(N)时间处理一个merge
定义
堆中每个节点,左儿子的npl >= 右儿子的npl
操作
merge
insert
deleteMin
性质
左儿子npl >= 右儿子npl
skew heap(斜堆)
有堆序性
定义
不维护npl
每次合并都交换左右(只有左儿子的除外)
其它同左式堆
性质
任意M次连续操作, 总的最坏情况运行时间为O(MlogN), 每次摊开销为O(logN)
操作
merge
insert
deleteMin
binomial queue(二项树)
B(k) 由B(0), B(1), ... B(k - 1)连接根组成
有2^k个节点, k为高度
pairing heap(配对堆)
fibonacci heap(斐波那契堆)
算法
heapsort(堆排序)
merge(合并)
概念
graph
vertices(结点)
edge(边)
# 是结点对偶的集合
endpoint(端点)
# 边(u, v)的端点u, v
incident(关联)
# u, v和边(u, v)关联
尾(tail)头(head)
# 边(u, v)离开u进入v, u是尾, v是头
loop(环)
# 连接顶点自身的边,只考虑不含圈的图
cycle(圈)
# 长至少1的路径
acycle(无圈的)
DAG(无圈图)
adjacent(邻接)
# (i, j)则i, j邻接
directed(图是有向的)
# 对偶<i, j>与对偶<j, i>不同
digraph(有向图)
undirected(无向的)
# 边表示为(i, j)
network(网络)
# 边上有成本的图
weighted graph(加权图)
# weighted digraph(加权有向图)相同
weight(权重)
cost(成本)
度
# 点的邻接点的数目
出度
# 有向图中,用该点作为第一个成分的边数目
path(路)
# 结点序列
cycle(环、回路)
# 首尾相同的简单路
acyclicity(无环性)
connected(连通的)
# 每一对结点间存在一条路
connectivity(连通性)
connected component(连通分量)
# 非连通图中包含的连通部分
underlying graph(基础图)
# 有向图去掉方向
strongly connected(强连通的)
# 有向图中, 一对结点都存在互相连通的路,则两点强连能
weakly connected(弱连通的)
# 有向图的基础图是连通的
strongly connected graph(强连通图)
# 所有结点对强连通
strongly connected components(强连通分量)
# 极大强连通子图
length(路的长度)
# 路的边数
simple path(简单路)
# 除首尾结点外,所有结点不同的路
directed path(有向路经)
complete(完全的)
# 任意两个顶点之间都有边相连,表示为K|V|
dense(稠密)
# 缺少边较少
connected(连通的)
biconnected(双连通的)
# 不存在割点(articulation point)
表示
V = {a, b, c, d, e, f}, E = {(a, c), (a, d), (b, c), (b, f), (c, e), (d, e), (e, f)}
|E|
# 边的数量
|V|
# 顶点的数量
adjacency matrix(邻接矩阵)
# 图的顺序表示法
无向图的邻接矩阵总是对称的
稠密图,邻接矩阵占空间小
weight matrix(权重矩阵)、cost matrix(成本矩阵)
adjacency list(邻接表)
# 图的链接表示法
稀疏图,邻接表占空间小
公式
0 <= |E| <= |V|(|V| - 1) / 2
# 无圈无向图,可能包含边的数量
算法
critical path analysis(关键路径分析法)
应用
activity-node graph(动作节点图)
event-node graph(事件节点图)
slack time(松弛时间)
critical path(关键路径)
 Oct 7, 2018
Oct 7, 2018
指数
#
X^A * X^B = X^(A + B)
X^A / X^B = X^(A - B)
(X^A)^B = X^(A * B)
X^N + X^N = 2X^N <> X^(2N)
2^N + 2^N = 2^(N + 1)
对数
#
约定
计算机科学中, log默认为log(2)
X^A = B, log(X)(B) = A
log(A)(B) = log(C)(B)/log(C)(A)
logAB = logA + logB
级数
#
∑(i=0)(N)2^i = 2^(N + 1) - 1
∑(i=0)(N)A^i = (A^(N + 1) - 1) / (A - 1)
如果0 < A < 1, 则 <= 1 / (1 - A)
∑(i=1)(∞)i/2^i = 2
∑(i=1)(N)i = N(N + 1) / 2 ≈ N^2 / 2
∑(i=1)(N)i^2 = N(N + 1)(2N + 1) / 6 ≈ N^3 / 3
∑(i=1)(N)i^k ≈ N^(k + 1) / |k + 1| k <> -1
k = -1时, Hn = ∑(i=1)(N)1 / i ≈ log(e)(N), Hn是调和级数
该近似式误差趋向于 λ ≈ 0.57721566, 称为欧拉常数(Euler's constant)
如果N整除A - B, 则称A与B模N同余, 记为A≡B(mod N)
81≡61≡1(mod 10)
如果A≡B(mod N), 则A + C ≡ B + C(mod N),则AD≡BD(mod N)
证明方法
#
归纳法
基准情形(base case)
归纳假设(inductive hypothesis), k成立
证明k + 1成立
反证法
无理数
#
圆周率π,黄金分割比ψ,重力加速度g,和自然对数的底e
# e约等于2.718281828
# e表示基础增长率为1时连续增长的实际增长率
## 连续增长是自然界最广泛、增长最快的一种
## ,所以e也表示自然增长速度, 也是增长的极限速度
e=lim(x→∞)(1+1/x)^x
例子
单细胞24小时分裂一次,x天产生2^x个细胞
加条件, 一天中新生细胞产生到一半(12小时)的时候自身可以分裂
一天产生2.25个细胞, 1个原有,1个新生, 0.25个是新生细胞分裂的
改条件,每8小时细胞具有分裂能力
一天可得到2.37个细胞
改条件,新生细胞每个细微时间都有分裂能力,一天最多可以产生的细胞
一天可得到e个细胞
例子2
e或e经过一定变换得到"自然律"
例子3
螺线φkρ=αe。其中,α和k为常数,φ是极角,ρ是极径,e是自然对数的底
pi = 3.
14159 26535 89793 23846 26433
83279 50288 41971 69399 37510
58209 74944 59230 78164 06286
20899 86280 34825 34211 70679
82148 08651 32823 06647 09384
46095 50582 23172 53594 08128
48111 74502 84102 70193 85211
05559 64462 29489 54930 38196
44288 10975 66593 34461 28475
64823 37867 83165 27120 19091
45648 56692 34603 48610 45432
66482 13393 60726 02491 41273
72458 70066 06315 58817 48815
20920 96282 92540 91715 36436
78925 90360 01133 05305 48820
46652 13841 46951 94151 16094
33057 27036 57595 91953 09218
61173 81932 61179 31051 18548
07446 23799 62749 56735 18857
52724 89122 79381 83011 94912
98336 73362 44065 66430 86021
39494 63952 24737 19070 21798
60943 70277 05392 17176 29317
67523
组合数学
#
原理
鸽巢原理、ramsey定理
概率
加法原理、乘法原理
排列组合、多重集排列组合
组合恒等式
容斥原理
多重集r-组合数
mobius反演
集合
集合分划 stirling数
生成函数
组合数
指数型
catalan数列与stirling数列
分拆数
递推关系
群
置换群
burnside引理
共轭类
不动置换类
等价类
polya定理
问题
幻方
拉丁方
涂色
非降路径
正整数分拆
无序分拆
ferrers图
分配
错位排列
棋盘多项式与有禁区的排列
离散数学
#
集合
c(0)(n) + c(1)(n) + ... + c(n)(n) = 2^n
# 幂集
关系r
子关系
逆
自反
对称、反对称
传递
乘积(合成)
自反闭包
等价
部分序
映射
原像、映像
满射、单射
基数(浓度)
逻辑
联结词
∨, ∧, ¬, ←, →, ↔
=, =>
# 等价,蕴涵
原子、公式、解释
范式
析取范式
合取范式
前束范式、skolem范式
谓词
∀, ∃
谓词演算
图
权图
dijkstra算法
树
最优树
kruskal、t*
有向图
euler路、euler图
无向图
hamilton路
平面图
kuratowski判定
同胚
平面图的euler公式
plato体
着色
匹配
二部图
增广路
最大匹配
konig无限性引理
王浩定理
计算机表示
邻接矩阵
关联矩阵
弧表表示
邻接表表示
星形表示
单源最短路径
dijkstra
bellman - ford
最大流问题
增广路定理
ford - fulkerson
最大容量增广路算法
dinic、dinic改进
最短增广路算法
一般的预流推进算法
最高标号预流推进算法
数论
辗转相除
质数
合同
剩余类
一次同余式
秦九韶定理
euler函数
一元高次同余式
二次剩余
legendre符号
euler判别法
二次剩余互反律
应用
加密
群
性质
封闭性 # 运算结果还在群中
结合律 # (a·b)·c = a·(b·c)
单位元(幺元) # e·a = a·e = a
逆元 # a·b = b·a = e
代数系统
半群
封闭性
结合律
幺半群
封闭性
结合律
幺元
置换群
轮换表
奇偶性
子群
循环群
右陪集
正规子群
lagrange定理
同态映射
同构映射
核
环
整数环、矩阵环、多项式环
消去环、交换环
整区
域
子环
理想
平凡理想
单纯环
极大理想
合同关系
环同态、同构
应用
计数问题
轨道
代表元素
burnside引理
纠错码
域
素域
多项式
根
有理域多项式
eisenstein定则
分圆多项式
有限域
格
x, ⊕
对偶原理
对偶表达式
同态、同构
几个分类
有界格
有余格
分配格
模格
布尔代数
有余分配格
stone定理
化简
quine
karnaugh图
语言
语法
# 任何3型语法都是2型语法...都是1型语法...都是0型语法
g = (v, t, s, p)
# v 字母表, t是v的一个终止符子集, s是v的一个元素初始符,p是产生式集合
0型语法
# 没有任何限制
1型语法
# 产生式如 w1 -> w2, w2长度大于等于w1, 或者 w1 -> λ
# 可以写 lw1r -> lw2r , 所以上下文有关
2型语法
# w1 -> w2, w1是单个非终止符
3型语法
# w1 -> w2, w1 = a 并且w2 = ab 或者w2 = a, 其中a, b为非终止符, a是终止符,也可以是λ
# 正则语法
演绎树
有输出的fsm
mealy机
moore
没有输出的fsm
kleeme闭包
终止状态
非确定fsm
转换确定fsm
语言识别
可识别集合(stephen kleene)
正则表达式
kleene定理
其它fsm
pushdown自动机
识别到上下文无关语法
线性有界自动机
识别到上下文有关语法
turing机
识别所有语法结构产生的语言,可实现任何算法
随机数学
#
概率
古典概型
几何概型
条件概率
全概率公式
bayes公式
bernoulli概型
随机变量
离散
连续
分布函数
概率密度
分布
(0 - 1)分布
二项分布
poisson分布
几何分布
均匀分布
指数分布
正态分布
二维
联合概率密度
边缘概率分布
边缘概率密度
二维正态分布
条件分布
卷积公式
n维
数字特征
期望、方差
cauchy - schwarz不等式
标准化随机变量
协方差
矩
k阶原点矩
k阶中心矩
k + l 阶混合原点矩
k + l 阶混合中心矩
协方差矩阵
n维正态分布
大数
chebyshev不等式
chebyshev定理
bernoulli定理
中心极限定理(levy - lindberg定理)
de moivre - laplace 极限定理
liapunov 定理
样本
样本分布函数
伽玛函数
χ2分布
t 分布
f 分布
参数估计
矩估计
最大似然估计
评选标准
无偏性
有效性
一致性
区间估计
置信下限、置信上限
正态总体参数的区间估计
两个正态区间估计
u估计
t估计
f估计
假设检验
显性检验
参数检验
正态总体参数
u检验
t检验
χ2检验
f检验
...
分布拟合检验
回归分析
一元线性回归
最小二乘
可线性化的回归方程
双曲线
幂函数
指数函数
倒指数
对数
s型曲线 1 / (a + b * e ^ -x)
多元线性回归模型
方差分析
单因素
双因素
交互作用双因素
正交试验
